

ĭefraigne, P., Dehant, V., Pâquet, P.: Link between the retrograde-prograde nutations and nutations in obliquity and longitude. 240, 159–172 (1990)ĭavies, M.E., Abalakin, V.K., Bursa, M., Hunt, G.E., Lieske, J.H., Morando, B., et al.: Report of the IAU/IAG/COSPAR working group on cartographic coordinates and rotational elements of the planets and satellites-1988. 202, 309–315 (1988)Ĭhapront-Touze, M.: Orbits of the Martian satellites from ESAPHO and ESADE theories. 114, 278 (1982)īretagnon, P., Francou, G.: Planetary theories in rectangular and spherical variables-VSOP 87 solutions. 345, 282–297 (1999)īretagnon, P.: Theorie du mouvement de l’ensemble des planetes (VSOP82). īouquillon, S., Souchay, J.: Precise modeling of the precession-nutation of Mars. 82, 129–141 (1980)īorderies, N., Balmino, G., Castel, L., Moynot, B.: Study of Mars dynamics from lander tracking data analysis. īorderies, N.: Theory of Mars rotation in Euler angles. ), our model predicts a dynamical flattening \(H_\) with \(h_0\) and \(k_0\) the constant parts of h and k.Īrchinal, B.A., Acton, C.H., A’Hearn, M.F., Conrad, A., Consolmagno, G.J., Duxbury, T., et al.: Report of the IAU Working Group on cartographic coordinates and rotational elements: 2015. Given the current determination of the precession rate ( \(7608.3\pm 2.1\) mas/yr, Konopliv et al. Uncertainties related to our modeling choices are negligible in comparison. The uncertainty on our solution mainly derives from the observational uncertainty on the current determination of the precession rate of Mars. With a truncation criterion of 0.025 milliarcseconds in prograde and/or retrograde amplitude, we identify 43 nutation terms. We use semi-analytical developments for the solar and planetary torques, and analytical solutions for the effect of Phobos and Deimos and for the geodetic precession and nutations. We also include the geodetic precession and nutations. We include in the model the forcings by the Sun, Phobos, Deimos, and the other planets of the solar system. Here, we develop such a model with adequate accuracy based on the Torque approach and compare it to previous models.
To avoid introducing systematic errors in the determination of the core properties, an accurate precession and nutation model for a rigidly behaving Mars is needed. The contribution to the nutations due to the liquid core and tidal deformations will be detected, allowing to constrain the interior of Mars.
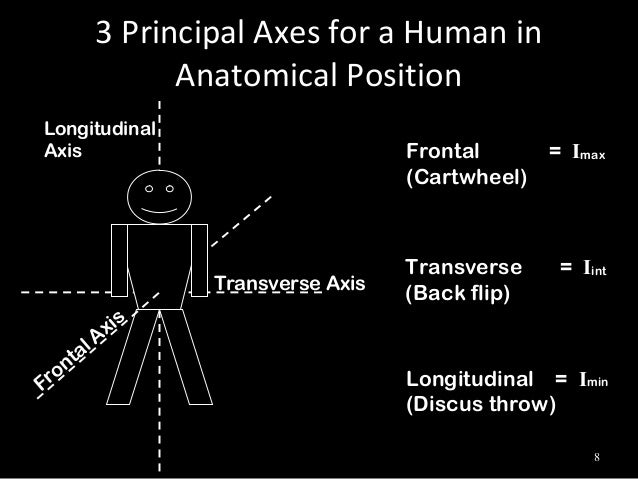
The moment of inertia depends on how mass is distributed around an axis of rotation, and will vary depending on the chosen axis.The nutations of Mars are about to be estimated to a few milliarcseconds accuracy with the radioscience experiments onboard InSight and ExoMars 2022. The moment of inertia plays the role in rotational kinetics that mass (inertia) plays in linear kinetics-both characterize the resistance of a body to changes in its motion.
#Calculate moment of inertia from precession period free#
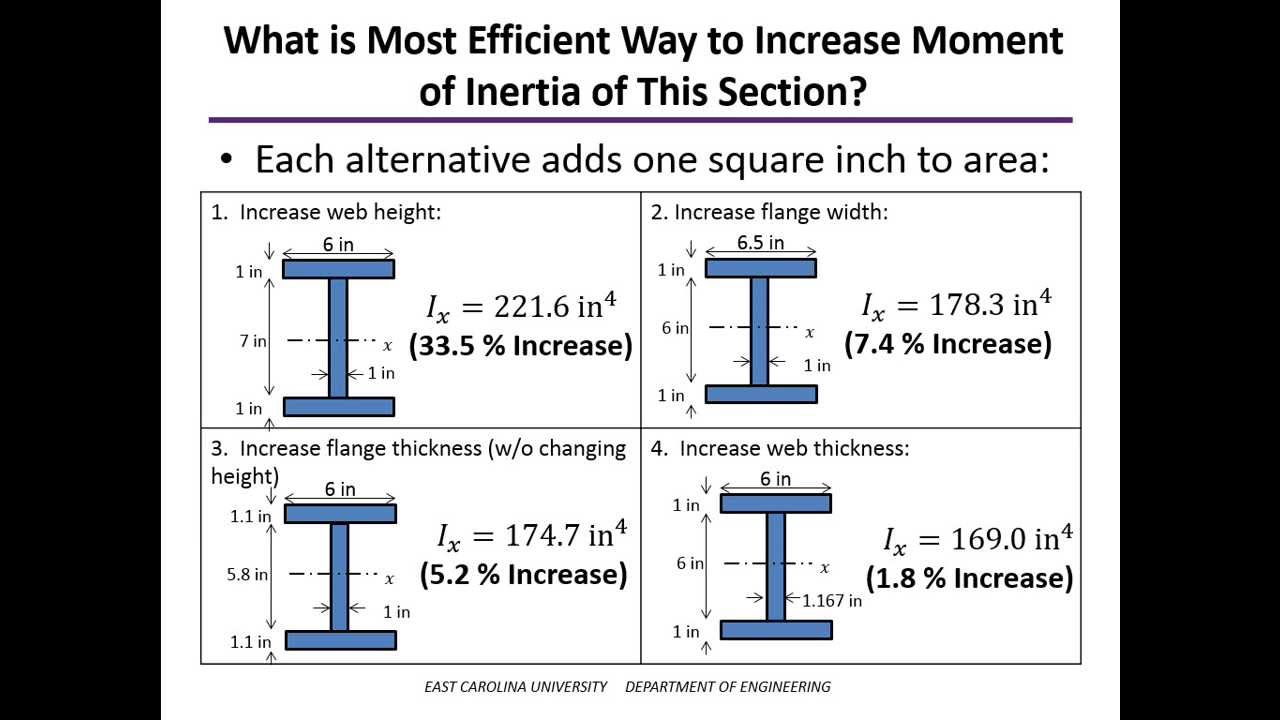
When a body is free to rotate around an axis, torque must be applied to change its angular momentum. For bodies free to rotate in three dimensions, their moments can be described by a symmetric 3-by-3 matrix, with a set of mutually perpendicular principal axes for which this matrix is diagonal and torques around the axes act independently of each other. Its simplest definition is the second moment of mass with respect to distance from an axis.įor bodies constrained to rotate in a plane, only their moment of inertia about an axis perpendicular to the plane, a scalar value, matters. The moment of inertia of a rigid composite system is the sum of the moments of inertia of its component subsystems (all taken about the same axis). It is an extensive (additive) property: for a point mass the moment of inertia is simply the mass times the square of the perpendicular distance to the axis of rotation. It depends on the body's mass distribution and the axis chosen, with larger moments requiring more torque to change the body's rate of rotation. The moment of inertia, otherwise known as the mass moment of inertia, angular mass, second moment of mass, or most accurately, rotational inertia, of a rigid body is a quantity that determines the torque needed for a desired angular acceleration about a rotational axis, akin to how mass determines the force needed for a desired acceleration. To improve their maneuverability combat aircraft are designed to have smaller moments of inertia than civil aircraft


 0 kommentar(er)
0 kommentar(er)
